Integral of E 2x
Now sin 2x dx -½ cos 2x. A soma de todas estas pequenas áreas áreas infinitesimais fornece a área entre.
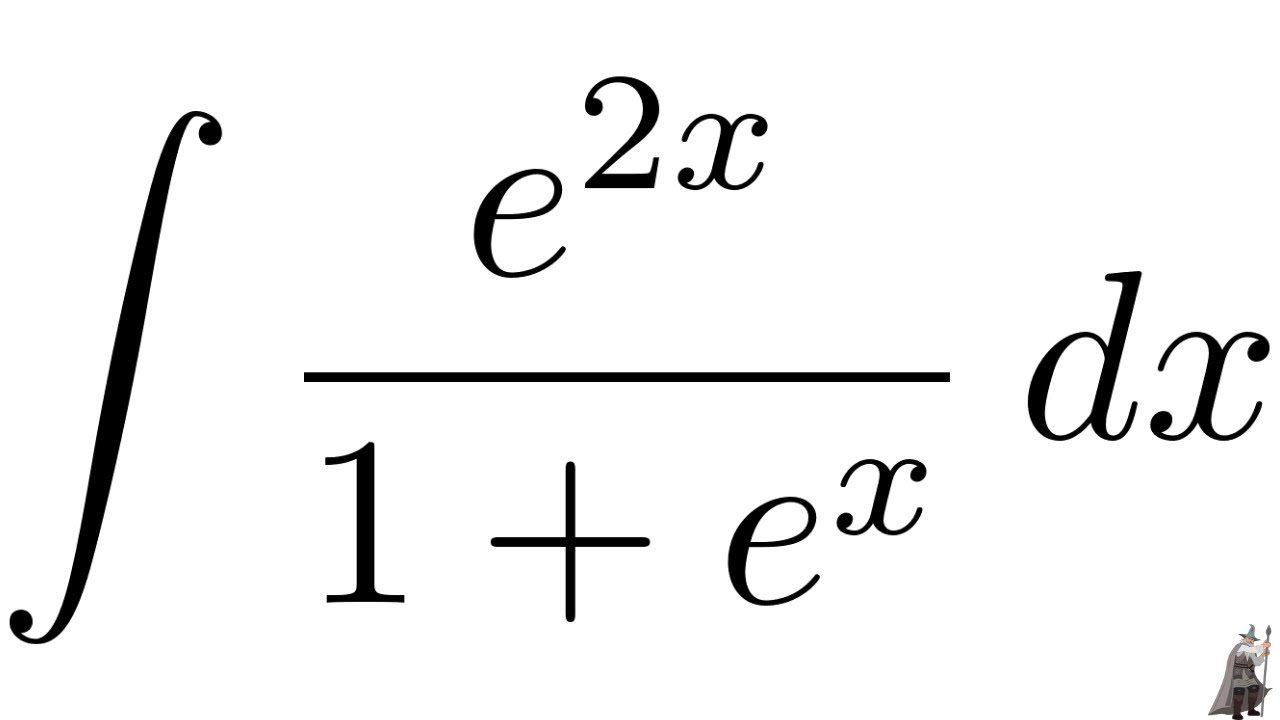
Integral E 2x 1 E X Math Methods Math Resources Free Math Resources
Advanced algebraic manipulations trig identities integration by parts with no product assume 1 as a multiplier.
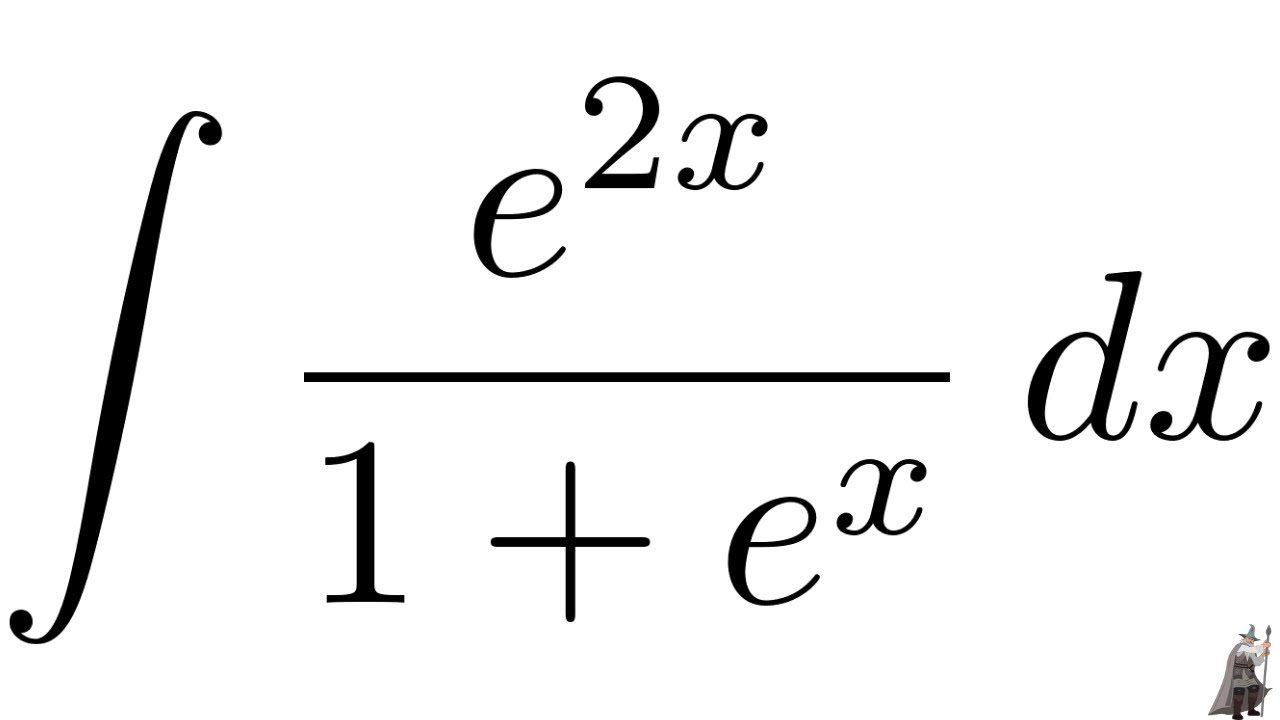
. To solve it there is a. Dy dx Pxy Qx. So the general solution of the differential equation is y Ae x Be 2x.
This formulation has proven crucial to. In this section R is an integral domain. U secn-2x Let db sec2x dx.
ǫ 1 Π2 e k2v2 1i π ω 2kv. Let I 0 π4 sin 2x dx. The process of finding the anti-derivative of a function is called integration.
1 e 3xdx Solution. The inverse process of finding derivatives is finding the integrals. For fx 4x raise the power of the variable by one and divide the entire function by the new exponent of the variable.
Also note that the notation for the definite integral is very similar to the notation for an indefinite integral. The characteristic equation is. A first order differential equation is linear when it can be made to look like this.
Solve d 2 ydx 2 3 dydx 2y e 3x. INTEGRAL CALCULUS - EXERCISES 45 62 Integration by Substitution In problems 1 through 8 find the indicated integral. Just as the derivative of ex is ex so the integral of ex is ex.
Note that the ein the integrand is a constant. By symmetry this is 2 R 0 xe x22dx. If none of the above techniques work you should take some more aggressive measures.
What is the second step of this standard normal MGF derivation. Definite integral is used to find the area volume etc. So in this case the fundamental solutions and their derivatives are.
Xn k is equal to the number of ways in which k identical balls can be distributed into N unique boxes such that each box must contain at-least 1 ball. R 2 3r 2 0. Given that X has density pdf fx 1x for 1 x 1 0 otherwise.
Calculate int_02left 3 x2 x - 1 rightdx. For defined range as a limit of sum. Π2 i ω2 1 3k2V2 ω2.
Substituting u 2x6and 1 2. Intleft3 x2 x - 1rightd xx3 fracx22 - x for steps see indefinite integral calculator According to the Fundamental Theorem of Calculus int_ab Fx dxfb-fa so just evaluate the integral at the endpoints and. Compute answers using Wolframs breakthrough technology knowledgebase relied on by millions of students professionals.
Begingroup You still need limits on the integral eg. From ǫ 0 we have 1 3k2V2 ω2 ω2 k2v2 s 1k2λ2 e i r π 2 ω Π ekλ e where v s λ eΠ i q ZT eM. These are precisely the invertible elements in RUnits divide all other elements.
Given elements a and b of R one says that a divides b or that a is a divisor of b or that b is a multiple of a if there exists an element x in R such that ax b. R 1 or 2. The units of R are the elements that divide 1.
R 1r 2 0. 30 where v and V are thermal velocities of electrons and ions respectively. Z e x3 e 3dx When working with exponential functions re-member to use the various rules of exponentia-tion.
Learn the properties formulas and how to find the definite integral of a given function with the help of examples only at BYJUS. When we speak about integration by parts it is about integrating the product of two functions say y uv. For an integral of the form tag1int_agx ftdt you would find the derivative using the chain rule.
For math science nutrition history. For example the integral of fx 4x becomes 2x 2. Differentiating an integral correctness and conditions.
They are First Order when there is only dy dx not d 2 y dx 2 or d 3 y dx 3 etc. If a divides b and b divides a then a and b are. Then du n 2 secn-2x tan x dx.
These anti-derivatives are also called the integrals of the function. More integral calculus concepts are given so keep learning integral formulas to solve problems accurately. Find the general solution of d 2 ydx 2 3 dydx 2y 0.
Number of positive integral solutions of equation x1 x2. We dont choose dv sec x dx because this would introduce a natural loganthm function a fearsome complication in the second integration. Insert the upper bound of the integral into the newly integrated function.
Also watch the video given below to clear your concept. First calculate the corresponding indefinite integral. For x 1 we use Gx 1i πx.
49e3 use integration by parts f R xex 22dx Solution. Where Px and Qx are functions of x. Here the rules.
A ideia desta notação utilizando um S comprido é generalizar a noção de somatório 4Isto porque intuitivamente a integral de sobre o intervalo pode ser entendida como a soma de pequenos retângulos de base tendendo a zero e altura onde o produto é a área deste retângulo. If we neglect V and imaginary part. The easiest power of sec x to integrate is sec2x so we proceed as follows.
Find initial integral solution of Linear. List of Integral Formulas. The list of basic integral formulas are.
13e3 e R 1 xe 3xdx Solution. Z 4 1 t2 dt Remember that the derivative of arctant is 1 1 t2. Find an integral solution of the non-linear equation 2X 5Y N.
Use trig substitution if the integral contains sqrta2x2 or sqrtx2-a2 for axb1n try simple substitution. Displaystyle int_0x instead of just displaystyle int and you really should use a different variable of integration than the one used in the limit. The reason for this will be apparent eventually.
The definite integral is defined to be exactly the limit and summation that we looked at in the last section to find the net area between a function and the x-axis. Integral calculus helps in finding the anti-derivatives of a function. Substituting u x2 du 2xdx this becomes R 0 e u2du 2 2.
Perform the integration of the function using indefinite integral rules. The integral of a function represents a family of curves. The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanicsIt replaces the classical notion of a single unique classical trajectory for a system with a sum or functional integral over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations. To express the given integral in terms of a lower power of sec x.

Integral Of E 2x 81 E 4x Using The Arctangent Function Math Videos Calculus Integration By Parts

Integral Of E X Sqrt 1 E 2x Using Trigonometric Substitution Math Videos Calculus Integration By Parts

Tabular Integration The Integral Of X 3 E 2x Math Videos Calculus Integrity
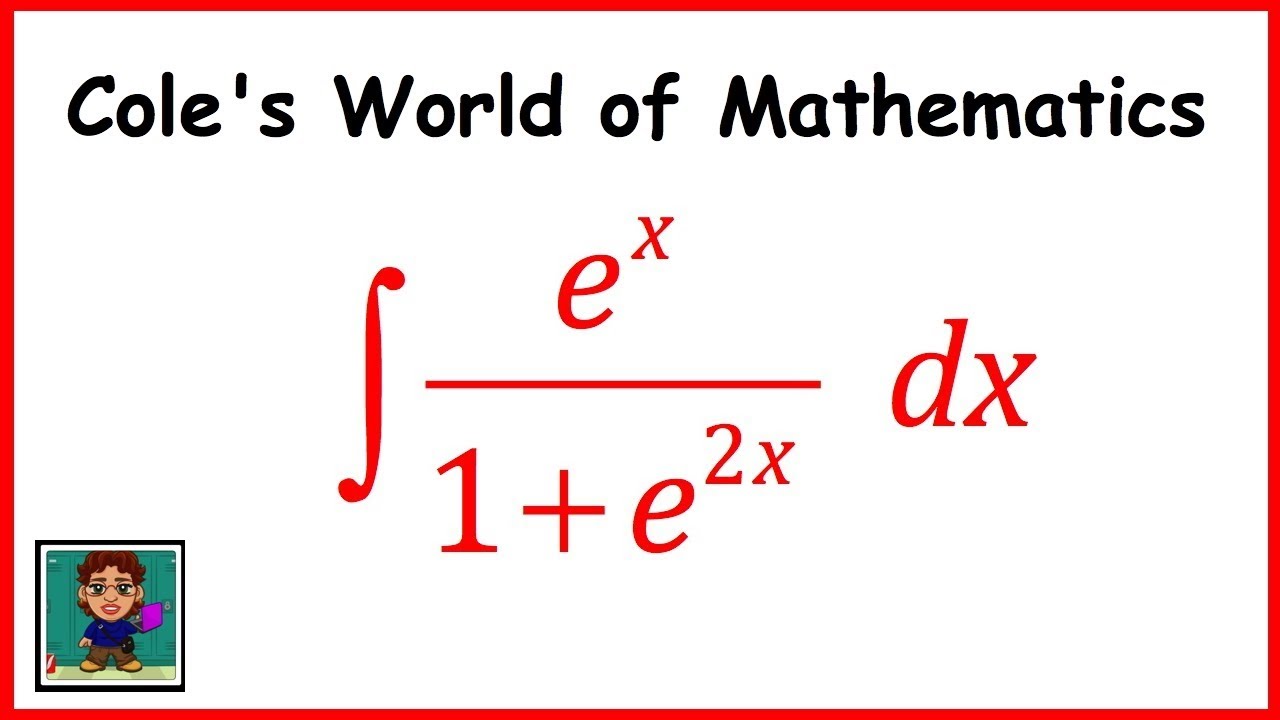
Integral Of E X 1 E 2x Calculus Calculus Mathematics Email Subject Lines
0 Response to "Integral of E 2x"
Post a Comment